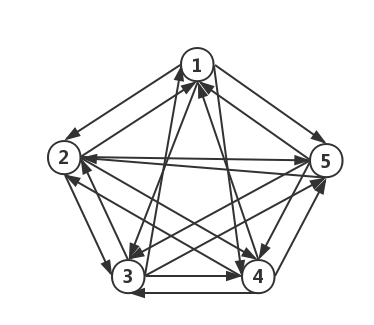
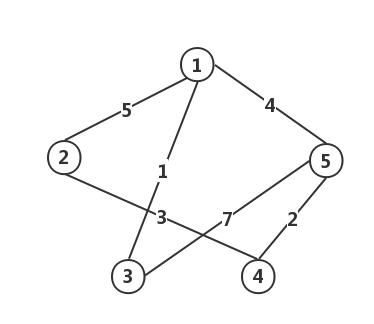
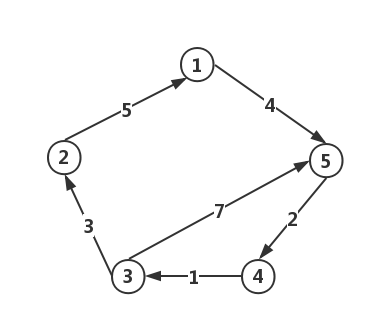
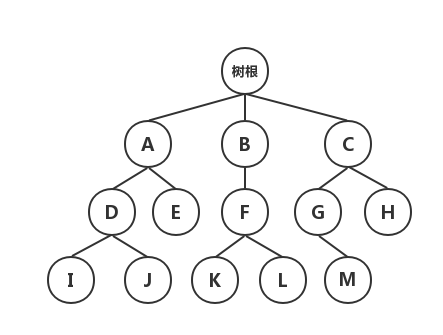
递归算法思想

递归算法（Recursion）就是在程序中不断反复调用自身来达到求解问题的目的。（这就要求待求解的问题能够分解为相同问题的一个子问题。）

注意：在递归函数中，必须使用 if 语句强制函数在未执行递归前返回。

分类

1. 直接递归：在函数中调用函数本身。
2. 间接递归：间接调用一个函数；如 fun_a 调用 fun_b, fun_b 又调用 fun_a。

示例

阶乘

阶乘，就是从 1 到指定数之间的所有自然数相乘的结果；n! = n x (n - 1) x (n - 2) x ... x 2 x 1 。推导：n! = n x (n - 1)!。

示例代码

1
2
3
4
5
6
7
8
9
10
11

#pragma mark -- 求自然数的阶乘
long Factorial(unsigned int n)
{
    if (1 >= n)
    {
        return 1;
    }
    long fact = Factorial(n - 1);
    
    return n * fact;
}

递推算法思想

递推算法（Derivation）是一种理性思维模式的代表，根据已有的数据关系，逐步推导而得到结果。执行过程如下：

1. 根据已知结果和关系，求解中间结果。
2. 判定是否达到要求，如果没有达到，则继续根据已知结果和关系求解中间结果。如果满足，则表示寻找到一个正确的答案。

示例

菲波那切数列（“兔子产仔”问题）

13世纪意大利数学家斐波那契的《算盘书》中记载了兔子产仔问题，其大意文如下：

如果一对两个月大的兔子以后每一个月都可以生一对小兔子，而一对新生的兔子生出两个月后才可以生小兔子。也就是说，1 月份出生，3 月份才可以产仔。那么假定一年内没有兔子死亡事件，那么 1 年后共有多少对兔子。

解析

• 第 1 个月：1 对兔子；
• 第 2 个月：1 对兔子；
• 第 3 个月：2 对兔子；
• 第 4 个月：3 对兔子；
• 第 5 个月：5 对兔子；
• 。。。

由此可以看出，从第 3 个月开始，每个月的兔子总数等于前两个月兔子数的总和：

穷举算法思想

穷举算法（Exhaustive Attack method）是最简单的一种算法，其依赖于计算机的强大计算能力来穷尽每一种可能的情况，从而达到求解问题的目的。其执行步骤如下：

1. 对于每一中可能的情况，计算其结果。
2. 判断结果是否满足要求，如果不满足则执行第 1. 步来搜索下一个可能的情况；如果满足要求，则表示寻找到一个正确的答案。

示例

鸡兔同笼问题

**”鸡兔同笼”**问题最早记载于 1500 年前的《孙子算经》，其原文如下：

今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？

题意：在一个笼子里关有若干只鸡和若干只兔，从上面数共有 35 个头，从下面数共有 94 只脚。问笼子里鸡和兔的数量各是多少？

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

/** 函数返回值 */
typedef enum {
    RetFailure          = 0,            // 失败
    RetSuccess          = 1,            // 成功
}RetValue;


#pragma mark -- 鸡兔同笼求值
RetValue ExhaustiveAttack(unsigned int headNum, unsigned int footNum, unsigned int* chicken, unsigned int* rabbit)
{
    if (0 == headNum || 0 == footNum)
    {
        return RetFailure;
    }
    for (unsigned int chNum = 0; chNum <= headNum; chNum++)
    {
        unsigned int raNum = headNum - chNum;
        
        if (footNum == chNum * 2 + raNum * 4)
        {
            *chicken = chNum;
            *rabbit  = raNum;
            return RetSuccess;
        }
    }

    return RetFailure;
}

图结构

图（Graph）结构也是是一种描述非线性关系的数据结构。在树结构中，结点之间是具有层次关系的，每一层的结点可以和多个下层结点关联，但是只能和一个上层结点关联。而图结构中，每个结点之间可以任意关联。

组成

1. 顶点（Vertex）：图中的结点。
2. 边（Edge）：图中连接结点的线。

所有的顶点构成一个顶点集合，所有的边构成一个边集合，一个完整的图结构就是由顶点集合和边集合组成。在数学上一般标记为：G = (V, E) 或者 G = (V(G), E(G))

注意：图结构中顶点集合 V(G) 必须为非空，即必须包含一个顶点；而边集合可以为空，此时表示没有边。

图的基本概念

1. 无向图：如果一个图结构中，所有边都没有方向性，则称为无向图（表示边时，对两个顶点的顺序没有要求，用圆括号表示：(V3, V4) ）。
   
2. 有向图：如果一个图结构中，边是有方向性的，则称为有向图（表示边时，对两个顶点的顺序有所要求，用尖括号表示：<V3, V4> ）。
   
3. 顶点的度（Degree）：连接顶点的边的数量称为该顶点的度（在无向图中，简单记为：D(V)；在有向图中，D(V) = OD(V) + ID(V) ）。
   • 出度：是以该顶点为端点的出边数量，记为：OD(V)。
   • 入度：是以该顶点为端点的入边数量，记为：ID(V)。
4. 邻接顶点：是指图结构中一条边的两个顶点（在有向图中，区分为：起始顶点（起点或始点）和结束顶点（终点） ）。
   • 入边邻接顶点：连接该顶点的边中的起始顶点。
   • 出边邻接顶点：连接该顶点的边中的结束顶点。
5. 无向完全图：如果在一个无向图结构中，每两个顶点之间都存在一条边，则称为无向完全图（N 个顶点的无向完全图，其总边数为：(N * (N - 1)) / 2）。
   
6. 有向完全图：如果在一个有向图结构中，每两个顶点之间都存在方向相反的两条边，则称为有向完全图（N 个顶点的有向完全图，其总边数为：(N * (N - 1))。
   
7. 子图：如果一个图结构的顶点和边都是另一个图结构的子集合，则称该图结构是另一个图结构的子图。
8. 路径：是指图结构中两个顶点之间的连线，路径上边的数量称之为路径长度。
   • 简单路径：在图结构中，如果一条路径上顶点不重复出现，则称之为简单路径。
   • 环（回路）：在图结构中，如果路径的第一个顶点和路径的最后一个顶点相同，则称之为环，有时也称之为回路。
   • 简单回路：在图结构中，如果除第一个顶点和最后一个顶点相同外，其余各顶点都不重复的回路称为简单回路。
9. 连通：如果图结构中，两个顶点之间有路径，则称这两个顶点是连通的（注意：连通的两个顶点可以不是邻接顶点，只要有路径连接即可，可以途径多个顶点）。
10. 连通图（无向图）：如果无向图中任意两个顶点都是连通的，则称之为连通图（如果无向图结构图中，包含两个顶点是不连通的，则称之为非连通图）。
11. 连通分量：无向图的极大连通子图（即任意连通子图都是连通分量）称为该图的连通分量。
12. 强连通图（有向图）：
    • 如果两个顶点之间有路径，也称为这两个顶点是连通的（注意：有向图中边是有方向的。因此，有时从 V1 到 V2 是连通的，但从 V2 到 V1 却不一定连通）。
    • 如果有向图中任意两个顶点都是连通的，，则称之为强连通图（如果有向图中包含两个顶点不是连通的，，则称之为非强连通图）。
13. 强连通分量：有向图的极大连通子图（即任意强连通子图都是强连通分量）称为该图的连通分量（强连通图只有一个强连通分量，那就是该图本事）。
14. 权（Weight）：在实际应用中需要将边表示成某种数值，这个数值便是该边的权（无向图中加入权值，则称之为无向带权图；有向图中加入权值，则称之为有向带权图）。
    
    
15. 网：网就是边上带有权值的图的另一种名称。

图的遍历

树结构

树（Tree）结构是一种描述非线性关系的数据结构。树是 n 个数据结点的集合，在该集合中包含一个根结点，根结点之下分布着一些互不交叉的子集合，，这些子集合也就是根结点的子树。

树结构的基本特征：

1. 在一个树结构中，有且仅有一个结点没有直接前驱（与其直接相连的前一个数据结点），这个结点就是树的 根结点。
2. 除根结点之外，其余每个结点有且仅有一个直接前驱。
3. 每个结点可以有任意多个直接后继（与其直接相连的后一个数据结点）。

从树的定义来看，树具有一种层次结构的性质；而从数学的角度来看，树具有一种递归的特性。

树结构的基本概念

• 父结点和子结点：每个结点的子树的根称为该结点的子结点；相应地，该结点被称为子结点的父结点。
• 兄弟结点：具有同一父结点的结点称为兄弟结点。
• 结点的度：一个结点所包含（直接）子树的数量。
• 树的度：该树所有结点中最大的（结点的）度。
• 叶结点：树中度为零的结点称为叶结点或终端结点。
• 分支结点：树中度不为零的结点称为分支结点或非终端结点。
• 结点的层数：结点的层数从树根开始计算，根结点为第1层、依次向下为第 2、3、…、n 层；树是一种层数结构，每个结点都处在一定的层次上。
• 树的深度：树中结点的最大层数称为树的深度。
• 有序树：若树中各结点的子树（兄弟结点）是按一定次序从左向右排的，称为有序树。
• 无序树：若树中各结点的子树（兄弟结点）未按一定次序从左向右排的，称为无序树。
• 森林：n(n > 0)棵互不相交的树的集合。

二叉树

二叉树（Binary Tree）是树结构的一种特殊形式，它是 n 个结点的集合，每个结点最多只能有两个子结点。二叉树的子树仍然是二叉树。二叉树一个结点对应的两棵子树分别称为左子树和右子树。由于子树有左右之分，因此二叉树是有序树。

队列结构

队列（Queue）是从数据的运算来分类的，按照 先进先出（First In First Out，FIFO） 的原则处理结点数据的。而从数据的逻辑结构来看，队列结构其实就是一种线性结构。

队列结构包括两类

1. 顺序队列结构：使用一组地址连续的内存单元依次保存队列中的数据。
2. 链式队列结构：使用链表形式保存队列中的数据。

(顺序)队列操作实例代码

数据准备

定义（顺序）队列结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

/** 队列的最大长度 */
#define MAX_LEN 100


/** 队列作返回值 */
typedef enum {
    RetError            = -1,           // 操作出错
    RetFailure          = 0,            // 操作失败
    RetSuccess          = 1,            // 操作成功
}RetValue;


/** 队列结点类型 */
typedef struct {
    char key[15];                       // 学号
    char name[20];                      // 姓名
    int age;                            // 年龄
}NodeData;


/** (顺序)队列结构 */
typedef struct {
    NodeData QueueData[MAX_LEN];        // 数据元素
    int head;                           // 队头位置（出队列）
    int tail;                           // 队尾位置（入队列）
}SQType;

（顺序）队列相关操作

栈结构

栈（Stack）是从数据的运算来分类的，按照 后进先出（Last In First Out，LIFO） 的原则处理节点数据的；在终端处理特别是重要数据的现场保护有着重要意义。而从数据的逻辑结构来看，栈结构其实就是一种线性结构。栈结构包括两类：

栈结构包括两类

1. 顺序栈结构
2. 链式栈结构

(顺序)栈操作实例代码

数据准备

定义（顺序）栈结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

/** 栈的最大长度 */
#define MAX_LEN 100


/** 链表操作返回值 */
typedef enum {
    Ret_Error           = -1,           // 操作出错
    Ret_NO              = 0,            // 操作失败
    Ret_YES             = 1,            // 操作成功
}RetValue;


/** 栈结点类型 */
typedef struct {
    char key[15];                       // 学号
    char name[20];                      // 姓名
    int age;                            // 年龄
}NodeData;


/** (顺序)栈结构 */
typedef struct {
    NodeData stackData[MAX_LEN];        // 数据元素
    int stackTop;                       // 栈顶位置
}SSType;

（顺序）相关操作

链表结构

链表（Linked List）结构是由许多结点依次链接而成，每个结点包括两部分：

1. 数据部分：保存的是该结点的实际数据
2. 地址部分：保存的是下一个结点的地址

链表分类

• 单链表：每个结点中只包含一个指针
• 双向链表：若每个结点包含两个指针，，一个指向下一个结点，另一个指向上一个结点
• 单向循环链表：在单链表中，将终端结点的指针域 NULL 改为指向头结点或开始结点
• 多重链的循环链表：如果将表中结点链在多个环上，将构成多重链的循环链表

(常规)链表操作实例代码

数据准备

定义链表结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

/** 链表操作返回值 */
typedef enum {
    RetError            = -1,           // 操作出错
    RetSuccess          = 0,            // 操作成功
} RetValue;


/** 链表结点类型 */
typedef struct {
    char key[15];                       // 学号
    char name[20];                      // 姓名
    int age;                            // 年龄
}NodeData;


/** 链表结构 */
typedef struct node {
    NodeData nodeData;                  // 保存结点数据
    struct node* nextNode;              // 保存下一结点的地址
}LLType;

顺序表结构

顺序表（Sequential List）是按照 顺序存储 方式存储的线性表，该线性表的结点按照逻辑次序依次存放在计算机的一组连续的存储单元中。

由于顺序表是依次存放的，只要知道该顺序表的首地址以及每个结点所占的存储长度，即可算出任何一个结点的位置。假设顺序表中开始结点 a1 的存储地址是 LOC(a1) ，每个结点占用存储空间为 C,则结点 ai 的存储地址计算公式为：LOC(ai) = LOC(a1) + (i - 1) * C (1 <= i <= n)

顺序表操作实例代码

数据准备

定义顺序表结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

/** 顺序表最大长度 */
#define MAX_LEN 100
	
	
/** 顺序表操作返回值 */
typedef enum {
    RetError            = -1,           // 操作出错
    RetSuccess          = 0,            // 操作成功
} RetValue;
	
	
/** 顺序表节点类型 */
typedef struct {
    char key[15];                       // 学号
    char name[20];                      // 姓名
    int age;                            // 年龄
}NodeData;
	
	
/** 顺序表结构 */
typedef struct {
    NodeData listData[MAX_LEN];         // 保存顺序表的结构数组
    unsigned int listLen;               // 顺序表已有节点的数量
}SLType;

相关操作

初始化顺序表

锯齿

Aliasing：走样（又称为“锯齿”），是指在模型边缘有锯齿的现象，在图形渲染中很常见，如下图：

Anti-Aliasing：反走样(常称“抗锯齿”)，是指要消除模型边缘锯齿的现象，让边缘看起来更加平滑，更真实。

出现锯齿现象是不可避免，是因为渲染物体时，需要将物体模型具体的位置坐标值转换成屏幕某个像素的值；物体模型的顶点坐标是可以任意的，而屏幕的由于像素的限制，只能转换成一定的值。当绘制3D物体的时候，计算物体的边缘位置，如果这个位置把大半个像素包括进去了，显示器会将这个像素设置成3D物体的颜色，如果没有包一半以上，这个像素就会设置成背景色。

多重采样

光栅器：是位于最终处理过的顶点之后到片段着色器之前所经过的所有的算法与过程的总和；作用是将一个图元的所有顶点作为输入，并将它转换为一系列的片段。

在光栅化阶段中，顶点坐标可以是任意的，但是片段(像素)不是，受限于分辨率。所以，绝大多数情况下，顶点和片元不会是完美的一一对应关系，所以光栅化的过程会确定图元的边界位置。如下图：

框框内红色或者黑色的点被成为采样点（注意：采样点不是像素）。默认情况下，采样点只有一个（单点采样），在片元中心。所以边界只有在包括一半以上的片元时才能将这个片元涂成物体的颜色。图中的三角形光栅化之后的结果如下图所示：