拿硬币问题
问题:
16个硬币,A和B轮流拿走一些,每次拿走的个数只能是1,2,4中的一个数。谁最后拿硬币谁输。请问:A或B有无策略保证自己赢?解答:
B可以保证自己赢。1
2
3
4
5
61. 如果A拿 1 个,则B拿 2 个;
2. 如果A拿 2 个,则B拿 1 个;
3. 如果A拿 4 个,则B拿 2 个。
4. 这样每次AB加起来都是 3 或者 6 ,所以最后会剩下 1 个或 4 个。
5. 如果是 1 个则A直接输了;
6. 如果剩下 4 个,A全拿则输了,如果不全拿,B继续采取上面的策略,最后还是剩下 1 个,还是A输。
分蛋糕问题
- 问题:请把一盒蛋糕切成
8份,分给8个人,但蛋糕盒里还必须留有一份。 - 解答:把切成的8份蛋糕先拿出7份分给7人,剩下的1份连蛋糕盒一起分给第8个人。
火车运煤问题
问题:你是山西的一个煤老板,你在矿区开采了有
3000吨煤需要运送到市场上去卖,从你的矿区到市场有1000公里,你手里有一列烧煤的火车,这个火车最多只能装1000吨煤,且其能耗比较大,每一公里需要耗一吨煤。请问,怎么运送才能运最多的煤到集市?解答: 。
1
2
3
41. 装 1000 吨煤,走 250 公里,扔下 500 吨煤,回矿山;
2. 装 1000 吨煤,走到 250 公里处,拿起 250 吨煤继续向前到 500 公里处,扔下 500 吨煤,回矿山。此时火车上还有 250 吨,再加上在 250 公里处还有 250 吨煤,所以,火车是可以回矿山的;
3. 装上最后 1000 吨煤,走到 500 公里处,装上那里的 500 吨煤,然后一直走到目的;
4. 由此,最多可以运送 500 吨煤到市场(当然,火车也回不去了,因为那矿山没有煤了)。
箱子开锁问题
问题:A、B两人分别在两座岛上。B生病了,A有B所需要的药。C有一艘小船和一个可以上锁的箱子。C愿意在A和B之间运东西,但东西只能放在箱子里。只要箱子没被上锁,C都会偷走箱子里的东西,不管箱子里有什么。如果A和B各自有一把锁和只能开自己那把锁的钥匙,A应该如何把东西安全递交给B?
解答:。
1
2
3
41. A 把药放进箱子,用自己的锁把箱子锁上;
2. B 拿到箱子后,再在箱子上加一把自己的锁;
3. 箱子运回 A 后,A 取下自己的锁;
4. 箱子再运到 B 手中时,B 取下自己的锁,获得药物。
吃药片问题
问题:某种药方要求非常严格,你每天需要同时服用A、B两种药片各
一颗,不能多也不能少。这种药非常贵,你不希望有任何一点的浪费。一天,你打开装药片A的药瓶,倒出一粒药片放在手心;然后打开另一个药瓶,但不小心倒出了两粒药片。现在,你手心上有一颗药片A,两颗药片B,并且你无法区别哪个是A,哪个是B。你如何才能严格遵循药方服用药片,并且不能有任何的浪费?解答:。
1
2
3
41. 把手上的三片药各自切成两半,分成两堆摆放;
2. 再取出一粒药片 A,也把它切成两半,然后在每一堆里加上半片的 A;
3. 现在,每一堆药片恰好包含两个半片的 A 和两个半片的 B;
4. 一天服用其中一堆即可。
老虎吃羊问题
问题:在岛上有100只老虎和1只羊,老虎可以吃草,但他们更愿意吃羊。如果每次只有一只老虎可以吃羊,而且一旦他吃了羊,他自己就变成羊;而且所有的老虎都是聪明而且完全理性的,他们的第一要务是
生存。 请问最后这只羊会不会被吃?如果是n只老虎和一只羊呢?解答:
1
2
3
41. 1 只老虎,肯定吃;
2. 2 只老虎肯定不吃,否则就被另一只吃了;
3. 3 只老虎,如果一只老虎吃掉了羊,这样问题就转换为 2 只老虎和 1 只羊的情况,显然另外两种老虎不敢轻举妄动,所以羊会被吃;
4. 4 只老虎,如果某一只老虎吃了羊,问题转化为 3 只老虎和 1 只羊的问题,它肯定会被接下来的某一只吃掉,然后其他两只只能等着,所以 4 只老虎,大家都不敢吃羊;归纳:我们就可以发现如果老虎数目是
奇数,那么羊肯定被吃,如果是偶数,那么羊肯定不会被吃。
假钱亏损问题
问题:王小姐是卖鞋的,一双鞋进货价45元,甩卖30元。顾客来买
两双鞋给了一张100元,王小姐没有零钱,于是找了邻铺兑换了100元零钱,找给顾客40元。事后邻铺发现钱是假的,王小姐无奈又赔了邻铺100元。请问,王小姐一共亏了多少元?解答:亏
130元1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19解法一:
1. 假定王小姐一开始有 200 元,进了 2 双鞋,45 * 2 = 90 此时她还剩 200 - 90 = 110;
2. 现在王小姐把鞋以 30 元一双的价格甩卖,2 双卖出后进账 30 * 2 = 60;
3. 王小姐没有零钱,用 100 换了邻居 100,钱数没有变化,此时王小姐手中有 110 + 60 = 170;
4. 这时邻居发现钱是假的,王小姐赔给邻居 100 元,此时王小姐手中钱数为 170 - 100 = 70;
5. 王小姐手中一开始有 200,最后剩 70,赔了 200 - 70 = 130;
6. 所以得出,王小姐亏了 130 元 。
解法二:
1. 王小姐收到一张 100 元假钞 (没得没失,所以是 0 );
2. 王小姐把 100 元假钞给邻居,换回 100 元真钞 (假钞换真钞,得到了 100 );
3. 王小姐把 2 双 90 元成本的鞋还有 40 元找零给了顾客 (失去了 90 + 40 = 130 元);
4. 王小姐被邻居发现那张一百是假的,于是只得赔给邻居 100 元 (失去了 100 元,先前用假钞换来的);
5. 所以王小姐最终亏了 130 元。
解法三:
1. 换钱的邻铺并没有赚钱,也没赔钱;
2. 使假币的顾客相当于没花钱得到 2 双鞋(45 * 2 = 90)加上 40 元真币,所以相当于赚了 130 元;
3 所以最终是王小姐亏了 130 元。
赛马问题
- 问题:
25匹马,每匹马的速度都不一样。因为只有5条跑道,所以一次竞赛只能跑5匹马,问最少需要多少次竞赛才能找到最快的3匹马? - 分析:。
1 | 1. 25 = 5 * 5,首先将所有的马分为5组,每组5匹进行比赛; |
| 假设比赛结果 | 比赛次数 |
|---|---|
| 1>2>3>4>5 | 第1次 |
| 6>7>8>9>10 | 第2次 |
| 11>12>13>14>15 | 第3次 |
| 16>17>18>19>20 | 第4次 |
| 21>22>23>24>25 | 第5次 |
1 | 3. 将 1、6、11、16、21 再比一次,假设结果是: |
| 假设比赛结果 | 比赛次数 |
|---|---|
| 1>6>11>16>21 | 第6次 |
1 | 4. 那么接下来最快的三匹马只可能在以下马中产生; |
| 假设比赛结果 | 比赛次数 |
|---|---|
| 11>7>6>2>3 | 第7次 |
1 | 由此可得最快的三匹马是 1、11、7。 |
- 解答:至少需要
7次。
九点连十线问题
问题:在
9个点上画10条直线,要求每条直线上至少有三个点?解答:。
1
解法一:三横一竖 + 六斜 (如下图)
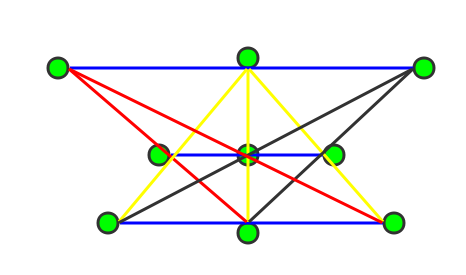
1
解法二:三竖一横 + 六斜(与解法一类似,如下图)
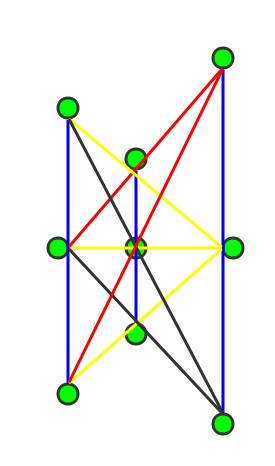
移动竹签问题
问题:如下图,只能移动两根竹签,而且形状不能改变,把围住的鸡蛋给移出来。(来自《少年包青天第一部》,第13集2分40秒 包拯到杂货店里买米,店老板出的题。)
解答:。
1
第一步:
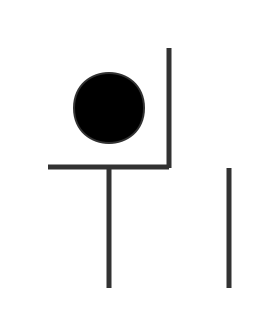
1
第二步: