C_C++常用数据结构和算法（十一）概率算法思想

概率算法思想

概率算法（Probability）依照概率统计的思路来求解问题；但往往不能得到问题的精确解，却是通过数值计算来求解近似值。

执行过程

1. 将问题转化为相应的几何图形 S，S的面积是容易计算的，问题的结果往往对应几何图形中某一部分 S1的面积。
2. 然后，向几何图形中随机撒点。
3. 统计几何图形 S 和 S1 的点数。根据 S 的面积和 S1 面积的关系以及各图形中的点数来计算得到结果。
4. 判断上述结果是否在需要的精度之内，如果未达到精度则执行步骤 2；如果达到精度则输出近似值。

算法的形式

1. 数值概率算法。
2. 蒙特卡罗（Monte Carlo）算法。
3. 拉斯维加斯（Las Vegas）算法。
4. 舍伍德（Sherwood）算法。

示例

蒙特卡罗（Monte Carlo）—— π 算法

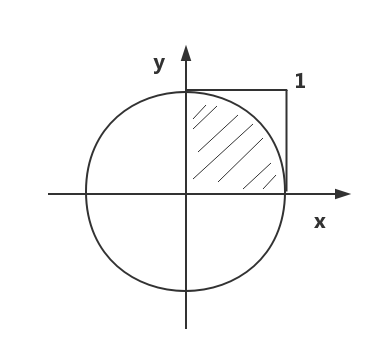
1. 如上图，设一个半径为 1 的圆，其面积为：S = π * r * r = π，（r == 1）。
2. 图中阴影部分是圆的 1/4，其面积为：S1 = S / 4 = π / 4。
3. 图中正方形的面积为：S2 = r * r = 1。

这样，按照图示建立一个坐标系，如果均匀地向正方形内撒点，那么落在阴影部分的点数与全部的点数之比应该是：S阴影 / S正方形 = π / 4。

根据概率统计的规律，只要撒的点足够多，那么将得到近似的结果。通过这个原理便可以计算圆周率 π 的近似值，这就是蒙特卡罗 π 算法。

注意： 使用蒙特卡罗算法计算圆周率有两个关键点：

1. 均匀撒点：在 C 语言中可以使用随机函数来实现，产生 [0,1] 之间随机的坐标值 [x,y]。
2. 区域判断：图中阴影部分的特点是距离坐标原点的距离小于等于 1，这样就可以通过计算判断：x*x + y*y <= 1 来实现。

示例代码

#pragma mark --  蒙特卡罗算法计算圆周率 π
double MonteCarloPI(int pointCount)
{
    double approximatePi;
    double x, y;
    int sum = 0;
    
    srand((unsigned)time(NULL));
    for (int i = 0; i < pointCount; i++)
    {
        x = (double)rand()/RAND_MAX;            // 产生 0 ~ 1 之间的一个随机数
        y = (double)rand()/RAND_MAX;            // 产生 0 ~ 1 之间的一个随机数
        if (1 >= x * x + y * y)
        {
            sum++;                              // 统计落在圆内的点
        }
    }
    approximatePi = 4.0 * sum / pointCount;     // 计算 π 近似值
    
    return approximatePi;
}

Demo下载