OpenGL学习笔记（十五）—— 投光物

投光物

投光物(Light Caster)：将光 投射(Cast)到物体的光源。

定向光

定向光(Directional Light)：一个处于无限远的光源（也叫做平行光），看似所有光线都朝着某一方向传播。

当一个光源处于很远的地方时，来自光源的每条光线就会近似于互相平行；不论物体和/或者观察者的位置，看起来好像所有的光都来自于同一个方向。（例如：太阳。）

通过定义一个光线 方向向量 而不是位置向量来模拟一个定向光。

定向光的判定

• 位置向量 定义为一个 vec4 时，必需将 w 分量设置为 1.0，这样 变换 和 投影 才能正确应用。
• 方向向量 定义为一个 vec4 时，必需将 w 分量设置为 0.0，这样 位移 时就不会有任何的效果（因为它仅仅代表的是方向）。

这样就可以通过检测 w分量 是否等于 1.0 来判断是光的 位置向量 还是光的 方向向量 了：（这正是旧 OpenGL（固定函数式）决定光源是定向光还是位置光源(Positional Light Source)的方法，并根据它来调整光照。）

if(0.0 == lightVector.w) // 注意浮点数据类型的误差
{
  // 执行定向光照计算
}
else if(lightVector.w == 1.0)
{
  // 根据光源的位置做光照计算
}

点光源

点光源(Point Light)：是一个朝着所有方向照射光线，但光线会随着距离逐渐衰减的光源；其能够配置位置和衰减（例如：灯泡）。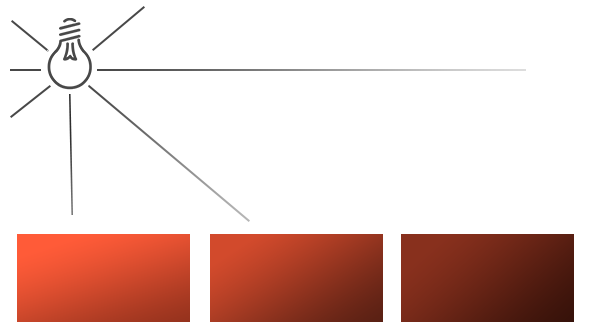

衰减

衰减(Attenuation)：随着光线传播距离的增长而光的强度逐渐削减的过程。

在现实世界中，灯在近处通常会非常亮，但随着距离的增加光源的亮度一开始会下降非常快，但在远处时剩余的光强度就会下降的非常缓慢了。根据现实现象，得出如下计算公式：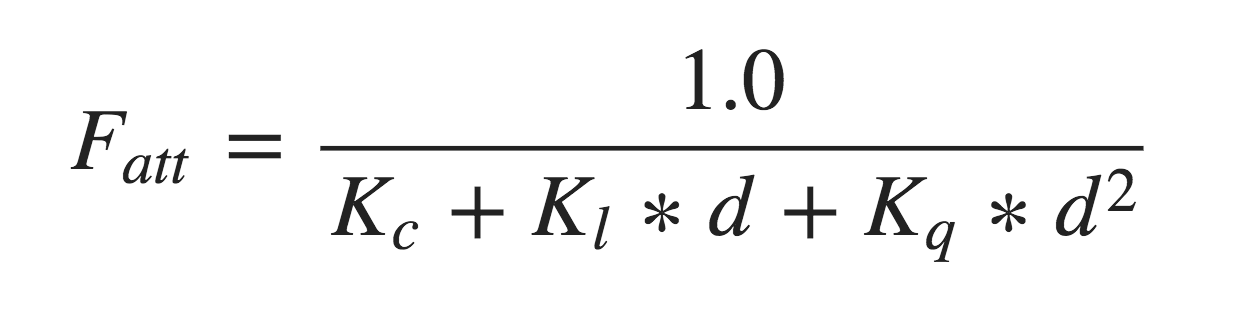

其中：

• d：表示片段距光源的距离；
• Kc：常数项，常数项通常保持为 1.0，这样就保证分母永远不会比 1 小，不然在某些距离上光强度反而会增加。
• Kl：一次项，与距离相乘，以线性的方式减少强度。
• Kq：二次项，与距离的平方相乘，让光源以二次递减的方式减少强度。（这样在距离比较小的时候衰减较小，当距离较大时衰减较大，比较符合现实现象。）

如下显示了在 100 的距离内衰减的效果：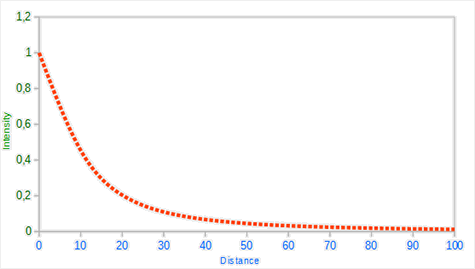

衰减公式数值选择

如下表格（来源于：Ogre Wiki）显示了模拟一个（大概）真实的，覆盖特定半径（距离）的光源时，这些项可能取的一些值：

(光照覆盖)距离：d	常数项：Kc	一次项：Kl	二次项：Kq
3250	1.0	0.0014	0.000007
600	1.0	0.007	0.0002
325	1.0	0.014	0.0007
200	1.0	0.022	0.0019
160	1.0	0.027	0.0028
100	1.0	0.045	0.0075
65	1.0	0.07	0.017
50	1.0	0.09	0.032
32	1.0	0.14	0.07
20	1.0	0.22	0.20
13	1.0	0.35	0.44
7	1.0	0.7	1.8

聚光

聚光(Spotlight)：是一个只朝某个特定方向(而不是所有方向)照射光线的光源；只有在聚光方向的特定半径内的物体才会被照亮，其它的物体都会保持黑暗（例如：手电筒、路灯）。

OpenGL 中聚光是用一个世界空间位置、一个方向和一个**切光角(Cutoff Angle)**来表示的，切光角指定了聚光的半径（是圆锥的半径不是距光源距离那个半径）。如图：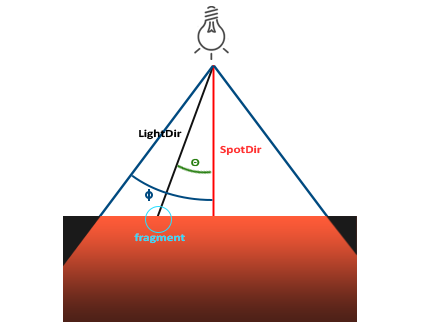

• LightDir：从片段指向光源的向量。
• SpotDir：聚光所指向的方向向量。
• ϕ（Phi）：指定了聚光半径的切光角，即圆锥半顶角(落在这个角度之外的物体都不会被这个聚光所照亮)。
• θ（Theta）：LightDir 向量和 SpotDir 向量之间的夹角。在聚光内部的话 θ 值应该比 ϕ 值小。

注意：在聚光计算中，通常通过计算 ϕ 和 θ 的余弦值进行比较。

手电筒

手电筒(Flashlight)：是一个位于观察者位置的聚光，通常它都会瞄准观察者视角的正前方（基本上说，手电筒就是普通的聚光，但它的位置和方向会随着观察者的位置和朝向不断更新。）。

平滑/软化边缘

对于聚光的硬边圈，需要模拟聚光有一个 内圆锥(Inner Cone) 和一个 外圆锥(Outer Cone)；内圆锥就是聚光显示的范围，外圆锥是用于控制聚光(强度)从内圆锥到外援追逐渐变暗的过程。

对于外圆锥，需要定义一个聚光方向向量 和 外圆锥向量 的夹角的 余弦值 ；如果片段处于内外圆锥之间，将计算出一个 0.0 到 1.0 之间的强度值，如果片段在内圆锥之内，强度就是 1.0，如果片段在外圆锥之外强度值就是 0.0。

由此，内圆锥到外援追之间的强度计算公式如下：

其中：

• θ（Theta）：LightDir 向量和 SpotDir 向量之间的夹角的 余弦值。
• ϕ（Phi）：内圆锥半顶角（内切光角）的 余弦值。
• γ（Gamma）：外圆锥半顶角（外切光角）的 余弦值。
• ϵ（Epsilon）：是 内圆锥（ϕ）和 外圆锥（γ）之间的 余弦值差（ϵ = ϕ − γ）。
• I：当前片段聚光的强度。

例如：（来自这里）

θ(余弦)	θ(夹角)	ϕ(余弦)	ϕ(内光切角)	γ(余弦)	γ(外光切角)	ϵ	I(聚光强度)
0.87	30	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.87 - 0.82 / 0.09 = 0.56
0.9	26	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.9 - 0.82 / 0.09 = 0.89
0.97	14	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.97 - 0.82 / 0.09 = 1.67
0.83	34	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.83 - 0.82 / 0.09 = 0.11
0.64	50	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.64 - 0.82 / 0.09 = -2.0
0.966	15	0.9978	12.5	0.953	17.5	0.966 - 0.953 = 0.0448	0.966 - 0.953 / 0.0448 = 0.29

Demo

---

参考

教程来源：https://learnopengl.com/。