坐标系统
OpenGL 每次在顶点着色器运行后,可见的所有顶点都为 标准化设备坐标(Normalized Device Coordinate, NDC)**;即每个顶点的 x,y,z 坐标都应该在 **[-1.0, 1.0] 区域之间,超出这个坐标范围的顶点都将不可见。然后将这些标准化设备坐标传入光栅器(Rasterizer),将其变换为屏幕上的二维坐标或像素。
在图形渲染管线(Pipe line)中,物体的顶点在最终转化为屏幕坐标之前还会被变换到多个坐标系统(Coordinate System),其中 5 个比较重要的坐标系统:
- 局部空间(Local Space,或者称为物体空间(Object Space))
- 世界空间(World Space)
- 观察空间(View Space,或者称为视觉空间(Eye Space))
- 裁剪空间(Clip Space)
- 屏幕空间(Screen Space)
坐标变换流程
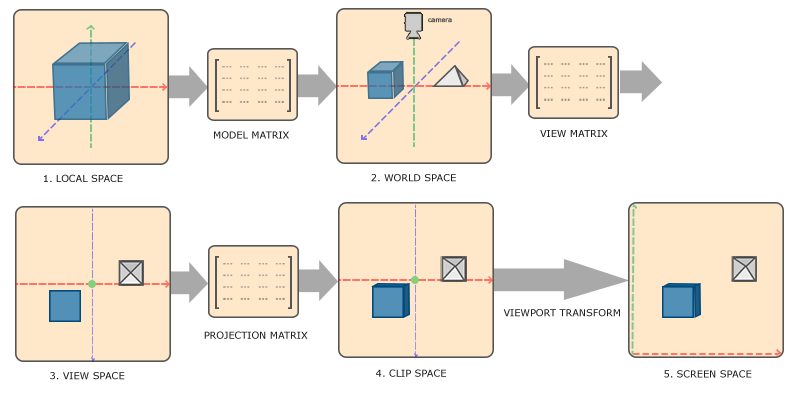
- 局部坐标是对象相对于局部原点的坐标,也是物体起始的坐标。
- 将局部坐标变换为世界空间坐标,世界空间坐标是处于一个更大的空间范围的。这些坐标相对于世界的全局原点,它们会和其它物体一起相对于世界的原点进行摆放。
- 将世界坐标变换为观察空间坐标,使得每个坐标都是从摄像机或者说观察者的角度进行观察的。
- 坐标到达观察空间之后,需要将其投影到裁剪坐标。裁剪坐标会被处理至
-1.0 到 1.0的范围内,并判断哪些顶点将会出现在屏幕上。 - 将裁剪坐标变换为屏幕坐标,进行**视口变换(Viewport Transform)**的过程。(视口变换将位于
-1.0到1.0范围的坐标变换到由glViewport函数所定义的坐标范围内;最后变换出来的坐标将会送到光栅器,将其转化为片段。)
局部空间
局部空间:是指物体自身所在的坐标空间,即对象最开始所在的地方。
世界空间
世界空间::是指顶点相对于(游戏)世界的坐标空间;使用模型矩阵通过对物体进行缩放、旋转、位移 操作将局部空间的坐标转变成世界空间的坐标。
观察空间
观察空间:是将世界空间坐标转化为用户视野前方的坐标空间;使用观察矩阵通过对物体进行 旋转、位移 操作将世界空间的坐标转变成观察空间的坐标。
裁剪空间
裁剪空间:是将观察空间的坐标在一定范围内进行裁剪的坐标空间;使用**投影矩阵(Projection Matrix)**将裁剪空间的坐标转变成裁剪空间的坐标。
当所有顶点被变换到裁剪空间,最终的操作——透视除法(Perspective Division) 将会执行,在这个过程中将位置向量的 x、y、z 分量分别除以向量的齐次 w 分量;透视除法是将 4D 裁剪空间坐标变换为 3D 标准化设备坐标的过程。(这一步会在每一个顶点着色器运行的最后被自动执行。)

正射投影
正射投影矩阵定义了一个类似立方体的平截头箱,定义了一个裁剪空间,在这空间之外的顶点都会被裁剪掉。(每个坐标的 w 分量没有改变。)
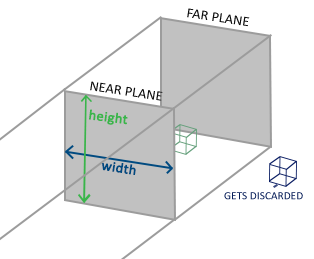
如图的平截头体由由宽、高、近(Near)平面和远(Far)平面所指定;任何出现在近平面之前或远平面之后的坐标都会被裁剪掉。
透视投影
使用 透视投影矩阵 来完成透视投影;这个投影矩阵将给定的平截头体范围映射到裁剪空间,除此之外还修改了每个顶点坐标的 w 值,从而使得离观察者越远的顶点坐标 w 分量越大。被变换到裁剪空间的坐标都会在 -w到w 的范围之间(任何大于这个范围的坐标都会被裁剪掉)。
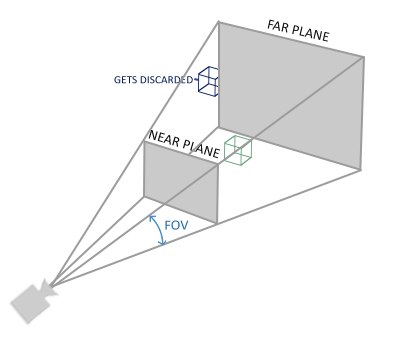
两者区别
使用透视投影的话,远处的顶点看起来比较小,而在正射投影中每个顶点距离观察者的距离都是一样的,如图:
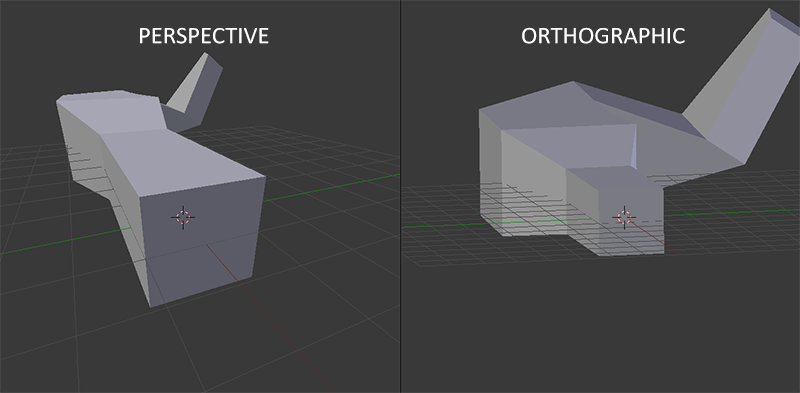
右手坐标系
按照惯例,OpenGL是一个右手坐标系,就是正 x 轴在右手边,正 y 轴朝上,而正 z 轴是朝向后方的。
右手坐标系法则:
- 沿着正
y轴方向伸出右手,手指着上方; - 大拇指指向右方;
- 食指指向上方;
- 中指向下弯曲90度。
那么大拇指指向正 x 轴方向,食指指向正 y 轴方向,中指指向正 z 轴方向。
效果